Convex Hull - Part 1

这学期有幸选到了贵系邓俊辉老师的《计算几何》，这学期会随着课程进度更新一些笔记。

凸包

用邓老师的话来说，所谓凸包就是

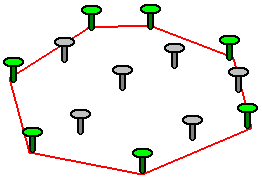
把点集看作钉在桌子上的若干钉子，这时撑开一个橡皮筋，让它能够囊括所有钉子，松手后橡皮筋围成的多边形就是该点集的凸包

当然这只是一个凸包在二维上的解释，但通俗易懂，如下图。

那么给定一个点集 $P$，如何计算出其凸包 $CH(P)$ 呢？接下来将介绍第一个计算凸包的算法 —— 极点法。

极点法（Extreme Points）

极点

如下图，对于点集中的某个点，若存在一条经过该点的直线，使得点集中的其余点均处于该直线的一侧，则称该点为极点（Extreme Point）。

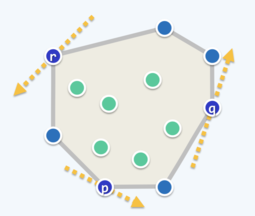
但根据上述定义很难实现凸包的构建算法，因为对于每个点都要遍历经过它的所有直线，而这些直线是无限的。

对于非极点来说，它必然会被点集中某三个点组成的三角形完全包围（不包括边界），而极点不满足该性质，如下图。

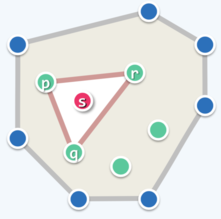
所以就可以遍历点集中的所有三角形，将其覆盖的所有点设置为非极点。通过排除所有的非极点就可以得到点集中的所有极点。 该算法的时间复杂度是 $O(C_{n}^{3}\cdot n)=O(n^4)$ 的。

那么如何判断点是否在三角形内呢？当然，可以使用射线法或累计角度法判定，但未免有些「杀鸡用牛刀」的意味。考虑边按逆时针排列的三角形，对于这三条有向边，若某点处于它们的左侧（toLeft 判断），则该点被该三角形覆盖，如下图。

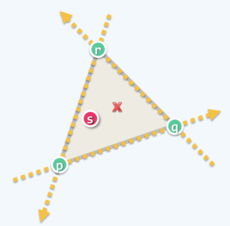
通过计算有向面积（$\times 2$）的符号能够判定某点是否在有向边的左侧：

$$2S=\begin{array}{|ccc|} p.x & p.y & 1 \\ q.x & q.y & 1 \\ s.x & s.y & 1 \end{array} \tag{1}$$

在得到点集中的所有极点后，再对它们进行排序（$O(n\log(n))$）就可以得到最终结果。

极点法虽然能够计算凸包，但还存在问题，其中最不能使人接受的是其较高的时间复杂度，之后将会介绍一些复杂度相对较低的算法。