Convex Hull - Part 3
这次继续介绍几个凸包算法,包括 Graham scan 和快速凸包算法。
Graham scan
Graham scan 是一个表达起来很简洁的算法,而且也没有涉及到复杂的数据结构,它仅仅需要两个栈 和 。
首先遍历所有点,选出 lowest-then-leftmost 的点 ,并以该点为参照,将所有其余点按照极角排序,分别为 。
两个栈初始化为(方括号代表栈底):
扫描算法流程:当栈 非空时,如果栈 的栈顶在栈 的栈顶与次栈顶组成的有向边的左侧,则将栈 的栈顶压入栈 ;否则弹出栈 的栈顶元素。伪代码如下:
while (!T.empty())
toLeft(S[1], S[0], T[0]) ? S.push(T.pop()) : S.pop();
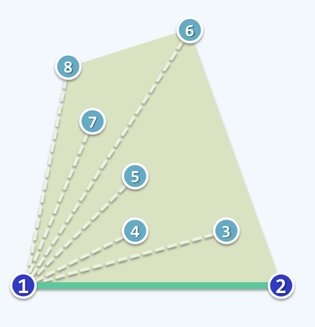
有兴趣的读者可以在下图所示的点集上运行一遍算法流程,我就不赘述了。
扫描效率
这一节讨论扫描一步的效率。粗浅来看,点集中除了参照点的每个点都可能被做 toLeft 比较,那么扫描效率就是 。但这种估计方法明显太松了,接下来用两种方法求更紧的上界。
平面图
先来复习一下图论中平面图的概念:
在图论中,平面图是可以画在平面上并且使得不同的边可以互不交叠的图。而如果一个图无论怎样都无法画在平面上,并使得不同的边互不交叠,那么这样的图不是平面图,或者称为非平面图。
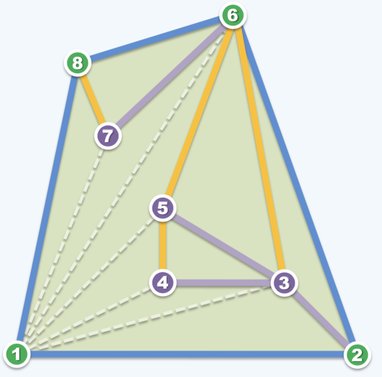
而在扫描一步中,遍历的所有边都不会相交(如下图)。也就是说,这一步的搜索空间构成了一个平面图。根据欧拉定理,得知平面图中边数 ,从而说明了扫描效率为 。
均摊分析
我们从另一方面看待这个问题,考虑变量 。显而易见地,每次循环中 都会减少 。扫描开始时,;扫描结束时,。则循环执行了 次,也即扫描效率为 。
简化
仔细想想,算法中的排序一步是不需要 toLeft 作为比较器的。
假如在点集中增加一个点作为参考点,并把它无限拉低,直到 ,则点集中其余点与参考点连成的线就是竖直的,也就是说,我们只需要对其余点的横轴坐标排序即可。
但由于引入了一个新的点,所以也会导致求得的凸包与原点集凸包不符。幸运的是,如果我们将新凸包中与参考点有关的两条边删掉,就可以得到原凸包的上半部分,称之为上半凸包(upper hull)。
同理,可以在点集中增加参考点 ,就可以求出下半凸包(lower hull)。将两者合并,就得到了原凸包。
极点个数期望
令 是平面上的点集,假设点的个数�是 ,这一节将讨论 (P的凸包)上点个数的量级。
值得注意的是,不同的采样方式会得出不同的结果。考虑在单位正方形内均匀且独立地采样(单位正方形与任意长方形是相同的,因为两者可以通过仿射变换至彼此)。
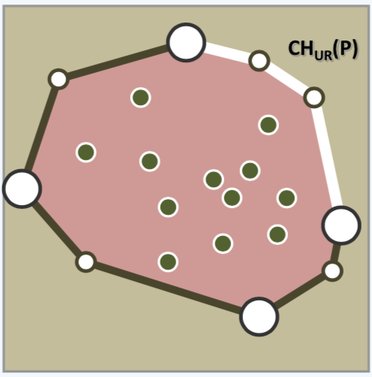
取凸包的最上/下/左/右四个点,可以将凸包分成四个部分,不失一般性,我们只考虑凸包的右上角 ,如下图。
在右上角区域,可以定义「极大点」:
以点 为原点建立坐标系,如果第一象限没有点集中的其余点,则称点 为极大点。
称极大点集为 ,则 ,接下来考虑 的期望。
从右到左,将点集中的点称之为 。对于点 来讲,它是极大点当且仅当它是 中最高的。由于点是在单位正方形内均匀独立采样得到的,则 是极大点的概率为 。故
经过上述推导,得知当在单位正方形内均匀独立采样时,凸包上点个数的期望为 。
除了在单位正方形内采样以外,在其他几何形状内采样则会得到不同的结果:
- 单位圆 —— ;
- 三角形 —— ;
- 凸 多边形 —— 。
快速凸包(Quickhull)
首先找出点集中 leftmost-then-lowest 的点 ,以及 rightmost-then-highest 的点 。则求解凸包就可以分为求解上半凸包和下半凸包,如下图。
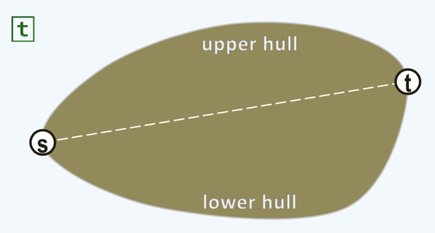
由于求解上下半凸包是对称的,所以只讨论上半凸包的求解过程。
与快速排序类似,在每次求解凸包时,都将当前点集分为三部分:
- 区域是需要被剪掉的部分,这其中的点之后无需考虑;
- 区域为左、右子区域,原凸包可以由这两个子区域的凸包组合而成。
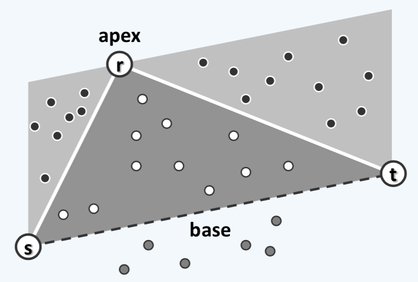
具体来说,取距离线段 最远的点 作为哨兵。那么 包围的区域则为 , 左侧的区域是 , 右侧的区域是 ,如�下图。
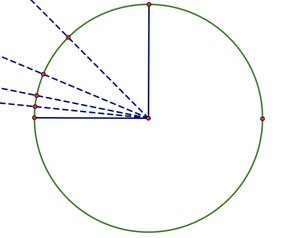
当然快速凸包算法的最差情况也是 的,考虑这种情况:在单位圆的直径上取两个点,随后在圆心角为 的位置加入点,如下图。那么每次选择哨兵时都会造成左右极不均匀,从而导致最坏情况。